Building a heap

Given an array with n elements, there are two ways to build a heap on it:

• Top-down
• Bottom-up

The top-down approach #

The first way is quite straightforward. We just do n insertions.

def build_heap_in_place(l):
    for i in range(len(l)):
        sift_up(l, i)

The part in [0, i) is the heap we have built so far. l[i] is the new element inserted.

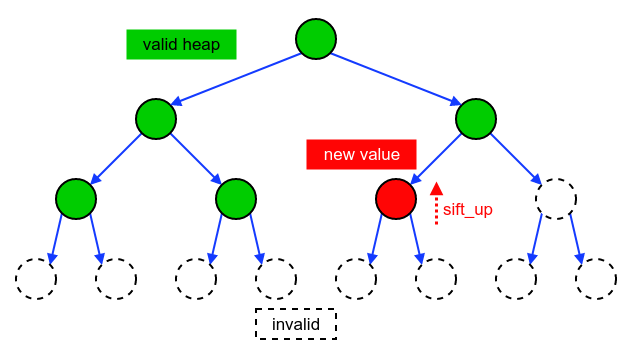
This approach runs in O(n*log(n)) time.

The bottom-up approach #

The second way runs in O(n), even in the worst case. ¹

def build_heap_in_place(l):
    for i in reversed(range(len(l)//2)): # skip leaves
        sift_down(l, i)

Why does it work? #

In the operation pop_max() (max heap), we move the last element to the top (heap_size -= 1), and call sift_down() on it.

Before the sift_down(), the new top node usually violates the heap property ( l[i] >= max(l[left_child(i)], l[right_child(i)]) ). However, the two subtrees of the top are both valid heaps.

What happens here in each iteration is quite similar.

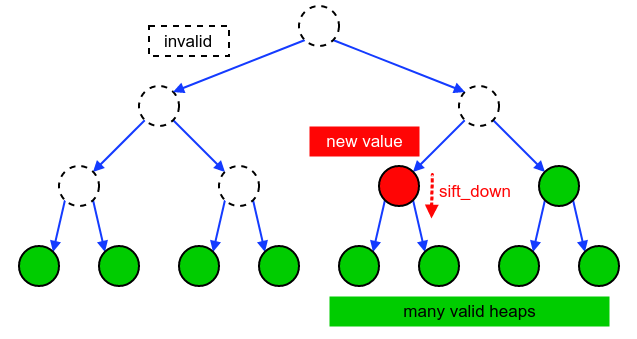
Complexity #

The time complexity of this approach is O(n) instead of O(n*log(n)), for there are exponentially more nodes at the bottom, which need less sift_down().²

• Last level: don’t need sift_down
• The second to last level: at most 1 sift_down
• The third to last level: at most 2 sift_down
• …

1 * n/4 + 2 * n/8 + 3 * n/16 + … = O(n)

Conclusion #

There are two approaches to build a heap.

The top-down approach:

• Can be considered as doing n insertions
• O(n*log(n))

The bottom-up approach:

• Associated with take_max()
• O(n)